Ábhar

• Céimeanna
• Modh 1 de 3: Conas cothromóid chiúbach a réiteach gan téarma seasmhach
• Modh 2 de 3: Conas Fréamhacha Iomlána a Aimsiú ag Úsáid Iolraitheoirí
• Modh 3 de 3: Conas Cothromóid a Réiteach ag Úsáid an Idirdhealaithe

I gcothromóid chiúbach, is é 3 an t-easpónant is airde, tá 3 fhréamh (tuaslagáin) ag cothromóid den sórt sin agus tá an fhoirm aici ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Níl sé éasca roinnt cothromóidí ciúbach a réiteach, ach má chuireann tú an modh ceart i bhfeidhm (le cúlra teoiriciúil maith), is féidir leat fréamhacha na cothromóide ciúbach is casta a fháil - chun an fhoirmle seo a úsáid chun an chothromóid chearnach a réiteach, faigh an fréamhacha iomlána, nó ríomh an idirdhealaitheach.

Céimeanna

Modh 1 de 3: Conas cothromóid chiúbach a réiteach gan téarma seasmhach

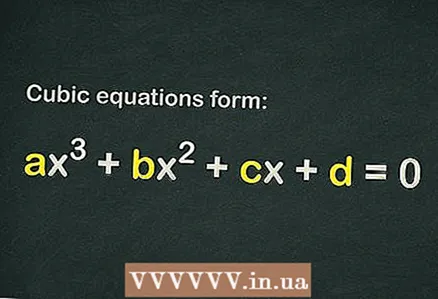1. 1 Faigh amach an bhfuil téarma saor in aisce sa chothromóid chiúbach d{ displaystyle d}. Tá an fhoirm ag an gcothromóid chiúbach ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Le go measfaí go bhfuil cothromóid ciúbach, is leor nach bhfuil ann ach an téarma ${ displaystyle x ^ {3}}$ (is é sin, b’fhéidir nach mbeidh baill eile ann ar chor ar bith).
   • Má tá téarma saor in aisce ag an gcothromóid ${ displaystyle d}$, bain úsáid as modh difriúil.
   • Más sa chothromóid é ${ displaystyle a = 0}$, níl sé ciúbach.
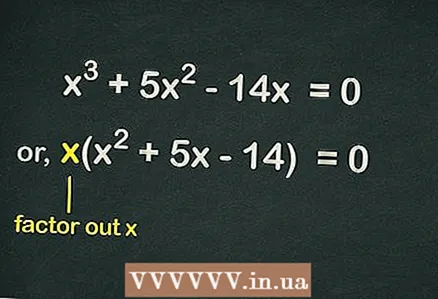2. 2 Tóg amach na lúibíní x{ displaystyle x}. Ós rud é nach bhfuil aon téarma saor sa chothromóid, tá an athróg san áireamh i ngach téarma sa chothromóid ${ displaystyle x}$... Ciallaíonn sé seo an ceann sin ${ displaystyle x}$ is féidir iad a eisiamh ó lúibíní chun an chothromóid a shimpliú. Mar sin, scríobhfar an chothromóid mar seo: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Mar shampla, má thugtar cothromóid chiúbach duit ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Tóg amach ${ displaystyle x}$ lúibíní agus a fháil ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
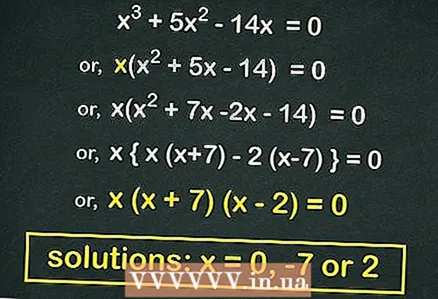3. 3 Fachtóir (táirge dhá dhéshúileach) an chothromóid chearnach (más féidir). Cothromóidí cearnacha go leor den fhoirm ${ displaystyle ax ^ {2} + bx + c = 0}$ is féidir a fhachtóiriú. Tiocfaidh cothromóid den sórt sin amach má thógann muid amach ${ displaystyle x}$ taobh amuigh de na lúibíní. In ár sampla:
   • Tóg amach na lúibíní ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Fachtóir an chothromóid chearnach: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Is ionann gach bosca bruscair agus ${ displaystyle 0}$... Is iad fréamhacha na cothromóide seo ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Réitigh cothromóid chearnach ag úsáid foirmle speisialta. Déan é seo mura féidir an chothromóid chearnach a fhachtóiriú. Chun dhá fhréamh cothromóide a fháil, luachanna na gcomhéifeachtaí ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ ionadach san fhoirmle ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • Inár sampla, cuir luachanna na gcomhéifeachtaí in ionad ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) isteach san fhoirmle:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • An chéad fhréamh:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • An dara fréamh:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Úsáid fréamhacha nialasacha agus cearnacha mar réitigh ar an gcothromóid chiúbach. Tá dhá fhréamh ag cothromóidí cearnacha, agus tá trí cinn ag ciúbach. Tá dhá réiteach aimsithe agat cheana féin - seo fréamhacha na cothromóide cearnacha. Má chuireann tú "x" lasmuigh de na lúibíní, bheadh ​​an tríú réiteach ${ displaystyle 0}$.
   • Má thógann tú "x" as na lúibíní, gheobhaidh tú ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, is é sin, dhá fhachtóir: ${ displaystyle x}$ agus cothromóid chearnach idir lúibíní. Má tá aon cheann de na fachtóirí seo ${ displaystyle 0}$, tá an chothromóid iomlán cothrom le ${ displaystyle 0}$.
   • Mar sin, tuaslagáin de chothromóid chiúbach iad dhá fhréamh de chothromóid chearnach. Is é an tríú réiteach ${ displaystyle x = 0}$.

Modh 2 de 3: Conas Fréamhacha Iomlána a Aimsiú ag Úsáid Iolraitheoirí

1. 1 Déan cinnte go bhfuil téarma saor in aisce sa chothromóid chiúbach d{ displaystyle d}. Más i gcothromóid den fhoirm é ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ tá ball saor in aisce ${ displaystyle d}$ (nach bhfuil cothrom le nialas), ní oibreoidh sé chun "x" a chur lasmuigh de na lúibíní. Sa chás seo, bain úsáid as an modh a leagtar amach sa chuid seo.
   • Mar shampla, má thugtar cothromóid chiúbach duit ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Chun nialas a fháil ar thaobh na láimhe deise den chothromóid, cuir ${ displaystyle 6}$ ar dhá thaobh na cothromóide.
   • Casfaidh an chothromóid amach ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Mar ${ displaystyle d = 6}$, ní féidir an modh a thuairiscítear sa chéad chuid a úsáid.
2. 2 Scríobh síos tosca an chomhéifeacht a{ displaystyle a} agus ball saor in aisce d{ displaystyle d}. Is é sin, faigh tosca na huimhreach ag ${ displaystyle x ^ {3}}$ agus uimhreacha roimh an gcomhartha comhionann. Thabhairt chun cuimhne gurb iad fachtóirí uimhreach na huimhreacha a tháirgeann an uimhir sin nuair a iolraítear iad.
   • Mar shampla, chun an uimhir a fháil 6, ní mór duit iolrú ${ displaystyle 6 times 1}$ agus ${ displaystyle 2 times 3}$... Mar sin na huimhreacha 1, 2, 3, 6 is fachtóirí den uimhir iad 6.
   • Inár gcothromóid ${ displaystyle a = 2}$ agus ${ displaystyle d = 6}$... Iolraitheoirí 2 atá 1 agus 2... Iolraitheoirí 6 an bhfuil na huimhreacha 1, 2, 3 agus 6.
3. 3 Roinn gach fachtóir a{ displaystyle a} do gach fachtóir d{ displaystyle d}. Mar thoradh air sin, faigheann tú a lán codáin agus roinnt slánuimhreacha; beidh fréamhacha na cothromóide ciúbach ar cheann de na slánuimhreacha nó luach diúltach ceann de na slánuimhreacha.
   • In ár sampla, roinn na tosca ${ displaystyle a}$ (1 agus 2) de réir tosca ${ displaystyle d}$ (1, 2, 3 agus 6). Gheobhaidh tú: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ agus ${ displaystyle { frac {2} {3}}}$... Anois cuir luachanna diúltacha na gcodán agus na n-uimhreacha a fuarthas leis an liosta seo: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ agus ${ displaystyle - { frac {2} {3}}}$... Tá fréamhacha iomlána na cothromóide ciúbach roinnt uimhreacha ón liosta seo.
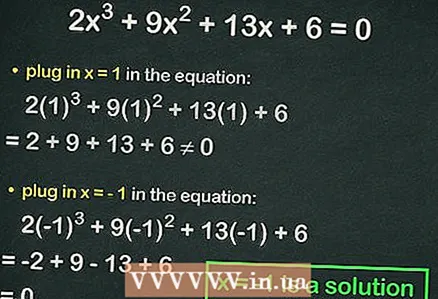4. 4 Breiseán slánuimhreacha isteach sa chothromóid chiúbach. Más fíor an comhionannas, is í an uimhir ionaid fréamh na cothromóide. Mar shampla, ionadach sa chothromóid ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, is é sin, ní thugtar faoi deara comhionannas. Sa chás seo, breiseán an chéad uimhir eile.
   • Ionadach ${ displaystyle -1}$: ${ displaystyle (-2) +9 + (- 13) +6}$ = 0. Mar sin, ${ displaystyle -1}$ is é fréamh iomlán na cothromóide.
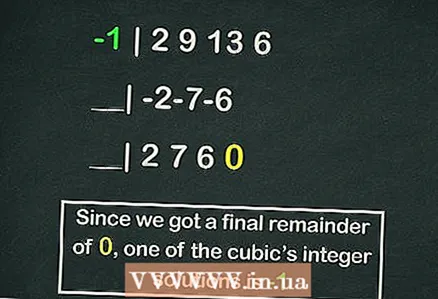5. 5 Úsáid an modh chun polynomials a roinnt ar Scéim Hornerchun fréamhacha na cothromóide a fháil níos tapa. Déan é seo mura dteastaíonn uait uimhreacha a chur sa chothromóid de láimh. I scéim Horner, roinntear slánuimhreacha de réir luachanna chomhéifeachtaí na cothromóide ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ agus ${ displaystyle d}$... Má tá na huimhreacha inroinnte go cothrom (is é sin, tá an fuílleach ${ displaystyle 0}$), is é slánuimhir fréamh na cothromóide.
   • Tá alt ar leithligh tuillte ag scéim Horner, ach seo a leanas sampla de cheann de fhréamhacha ár gcothromóid chiúbach a ríomh agus an scéim seo á húsáid:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Mar sin tá an chuid eile ${ displaystyle 0}$, ach ${ displaystyle -1}$ ar cheann de fhréamhacha na cothromóide.

Modh 3 de 3: Conas Cothromóid a Réiteach ag Úsáid an Idirdhealaithe

1. 1 Scríobh síos luachanna chomhéifeachtaí na cothromóide a{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} agus d{ displaystyle d}. Molaimid duit luachanna na gcomhéifeachtaí léirithe a scríobh síos roimh ré ionas nach gcuirfear mearbhall ort sa todhchaí.
   • Mar shampla, i bhfianaise na cothromóide ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$... Scríobh síos ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ agus ${ displaystyle d = -1}$... Thabhairt chun cuimhne más rud é roimhe seo ${ displaystyle x}$ níl aon uimhir ann, tá an chomhéifeacht chomhfhreagrach ann fós agus tá sí cothrom le ${ displaystyle 1}$.
2. 2 Ríomh an t-idirdhealaitheoir nialasach ag úsáid foirmle speisialta. Chun cothromóid chiúbach a réiteach ag baint úsáide as an idirdhealaitheach, ní mór duit roinnt ríomhanna deacra a dhéanamh, ach má dhéanann tú na céimeanna go léir i gceart, beidh an modh seo fíor-riachtanach chun na cothromóidí ciúbach is casta a réiteach. An chéad ríomh ${ displaystyle Delta _ {0}}$ (idirdhealaitheach nialasach) an chéad luach a theastaíonn uainn; chun é seo a dhéanamh, cuir na luachanna comhfhreagracha san fhoirmle in ionad ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Is é an t-idirdhealaitheoir uimhir arb iad is sainairíonna fréamhacha polaireimiceach (mar shampla, ríomhtar idirdhealaitheoir cothromóid chearnach leis an bhfoirmle ${ displaystyle b ^ {2} -4ac}$).
   • Inár gcothromóid:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Ríomh an chéad idirdhealaitheoir ag úsáid na foirmle Δ1=2b3−9abc+27a2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. An chéad idirdhealaitheach ${ displaystyle Delta _ {1}}$ - is é seo an dara luach tábhachtach; chun é a ríomh, breiseán na luachanna comhfhreagracha san fhoirmle shonraithe.
   • Inár gcothromóid:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Ríomh:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Is é sin, faigh idirdhealú an chothromóid chiúbach trí na luachanna a fhaightear ${ displaystyle Delta _ {0}}$ agus ${ displaystyle Delta _ {1}}$... Má tá idirdhealú cothromóid chiúbach dearfach, tá trí fhréamh ag an gcothromóid; más nialas an t-idirdhealú, tá fréamh nó dhó ag an gcothromóid; má tá an t-idirdhealú diúltach, tá fréamh amháin ag an gcothromóid.
   • Bíonn fréamh amháin ar a laghad i gcothromóid chiúbach i gcónaí, ós rud é go dtrasnaíonn graf na cothromóide seo an ais-X ag pointe amháin ar a laghad.
   • Inár gcothromóid ${ displaystyle Delta _ {0}}$ agus ${ displaystyle Delta _ {1}}$ cothrom ${ displaystyle 0}$, ionas gur féidir leat a ríomh go héasca ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Dá bhrí sin, tá fréamh nó dhó ag ár gcothromóid.

5. 5 Ríomh:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } deas) div 2}}}$. ${ displaystyle C}$ - is é seo an chainníocht thábhachtach dheireanach atá le fáil; cuideoidh sé leat fréamhacha na cothromóide a ríomh. Cuir na luachanna san fhoirmle shonraithe ${ displaystyle Delta _ {1}}$ agus ${ displaystyle Delta _ {0}}$.
   • Inár gcothromóid:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Faigh trí fhréamh den chothromóid. Déan é leis an bhfoirmle ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, cá ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, ach n cothrom le 1, 2 nó 3... Cuir na luachanna cuí san fhoirmle seo - mar thoradh air sin, gheobhaidh tú trí fhréamh den chothromóid.
   • Ríomh an luach ag baint úsáide as an bhfoirmle ag n = 1, 2 nó 3agus ansin seiceáil an freagra. Má fhaigheann tú 0 nuair a sheiceálann tú do fhreagra, is é an luach seo fréamh na cothromóide.
   • In ár sampla, ionadach 1 in ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$ agus a fháil 0, i.e. 1 ar cheann de fhréamhacha na cothromóide.